La transición al Cálculo

Es en el siglo XVII donde el desarrollo de las matematicas surge dramaticamente, Napies inventa los logaritmos, Harriot y Oughtred contribuyen a la codificacion y notacion del algebra, Galileo comienza el estudio de la dinámica y Kepler culmina el trabajo de Copernico estableciendo las leyes del movimiento de los planetas, Desargues y Pascal plantean bases de una nueva etapa en el desarrollo de la geometría culminando con Descartes y la geometria analítica. Fermat establece las bases de la teoría de números moderna, Huygens establece contribuciones imortantes a la probabilidad y es al final del siglo despues de toda esta preparación que se inventa el cálculo por Newton y Leibniz.

Newton 

Dentro de las primeras aportaciones al cálculo que como dato curioso es el concepto de integración el que surge en un principio. Tenemos a Zeno, Eudoxus' con su método de exhausión (Ver figura) y Arquimedes con el Método de Equilibrio plantea la idea conceptual basica para encontrar el área y volumen de un cuerpo geométrico. 

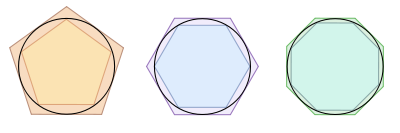
                        Metodo Exhaustivo